【今日の問題①】おうぎ形と三角形の問題

問題1

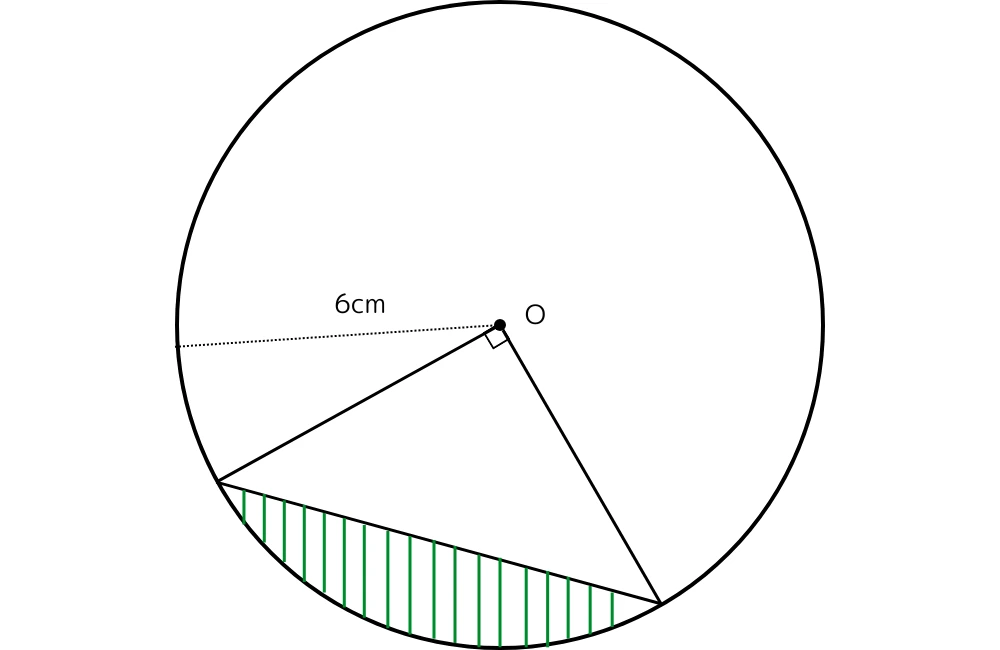
半径6cmの円があります。この円の中心角が90°のおうぎ形があり、さらにこのおうぎ形の内部に、円の中心と弧の両端を結ぶ二等辺三角形があります。おうぎ形の面積から二等辺三角形の面積を引いた部分（斜線部）の面積を求めなさい。円周率は$\pi$とします。

このような問題は、おうぎ形の面積から三角形の面積を引くことで、求めたい射線部の面積を求めることができます。

実際の解答例は下記のような手順で進めていきます。

この問題の円$O$の半径は6cmで、中心角が90°なので、おうぎ形の面積は

$6×6×\pi×\frac{90}{360}$

$=36×\pi×\frac{1}{4}$

$=9\pi$

よって、おうぎ形の面積は$9\pi$$cm^{2}$になります。

次に三角形の面積を求めていきます。

この問題では、円周角が90°であるため、おうぎ形の中にある三角形は直角二等辺三角形になります。

よって、三角形の面積は

$\frac{1}{2}×6×6$

=18

三角形の面積は18$cm^{2}$になります。

それぞれの面積が求まったので、射線部の面積は

$(9\pi-18)cm^{2}$となります。