中学2年生になると、「データの分布」という新しいテーマを学び始めます。
これは、単に平均や合計を計算するだけでなく、データ全体の広がりや偏り、そしてその特徴をどう表すかという点に焦点を当てた内容です。
現代社会では、学校の成績やスポーツの記録、気温の変化、企業の売上など、さまざまな場面でデータが使われています。
そのため、「データの分布」を正しく理解することは、数学の学習だけでなく、将来にわたって社会で役立つ大切なスキルにつながります。
特に、中学2年で新しく登場する「四分位範囲」と「箱ひげ図」は、多くの生徒にとって聞きなれない言葉ですが、データを比較したり特徴を捉えたりする上で重要な役割を果たします。
このページでは、これらの基礎を丁寧に解説し、意味や必要性を理解できるようにまとめていきます。
データの分布を学ぶ意味とは

まず、「データの分布」とは何を意味するのでしょうか。
分布とは、集めたデータがどのように散らばっているのか、つまり「広がり方」や「まとまり方」を表すものです。
たとえば、クラス全員の数学のテストの点数を調べるとします。
平均点が70点だったとしても、クラス全体が65点から75点の間に集まっている場合と、30点から100点まで大きくばらけている場合とでは、データの分布はまったく違います。
単に「平均70点」と言われても、その背景にあるデータの特徴まではわかりません。
そこで、「データの分布」を意識する必要があるのです。
こうしたデータの広がりを理解するために導入されるのが、四分位範囲や箱ひげ図といった考え方です。
これらを使うことで、平均だけでは見えない「データの全体像」がよりはっきりと見えてきます。
四分位範囲とは何か?

ここで、「四分位範囲とは」という疑問を持つ人は多いでしょう。
四分位範囲とは、データの散らばりを表す指標の一つで、データを「4つの等しい部分」に区切って、その真ん中の範囲を示すものです。
具体的には、データを小さい順に並べ、
- 第1四分位数(Q1) … 下から25%の位置の値
- 第2四分位数(Q2) … ちょうど真ん中(中央値)
- 第3四分位数(Q3) … 上から25%の位置の値
を求めます。
すると、Q1からQ3までの範囲が「四分位範囲」です。
数式で表すと、
四分位範囲 = Q3 – Q1
となります。
この四分位範囲は、データの真ん中50%がどの範囲に集中しているかを表しており、データの「ばらつき」を理解するのに役立ちます。
四分位範囲の意味と必要性
では、四分位範囲の「意味」と「必要性」を具体的に見てみましょう。
- 意味
四分位範囲とは、データの真ん中部分の広がりを表す数値です。
平均値だけでは極端な値(外れ値)に大きく左右されてしまいますが、四分位範囲を使えば、極端なデータの影響を受けずに、データ全体の傾向を把握できます。 - 必要性
四分位範囲の必要性は、データを公平に比較するためにあります。
例えば、2つのクラスのテスト結果が同じ平均点でも、四分位範囲を比較すると「どちらのクラスが成績のばらつきが小さいか(つまり学力の安定性があるか)」が分かります。
実際の社会でも、投資のリスク管理や商品の品質評価、さらにはスポーツ選手の成績分析など、多くの場面で「四分位範囲」を用いることで、より正確に状況を理解できます。
箱ひげ図とは何か?

次に登場するのが、「箱ひげ図」です。
箱ひげ図とは、データの分布をひと目でわかるように図で表したものです。
箱ひげ図では、以下の要素を組み合わせて描きます。
- 箱 … Q1からQ3までの範囲(=四分位範囲)
- 箱の中の線 … 中央値(Q2)
- ひげ … データの最小値と最大値
このように、箱ひげ図は「四分位範囲とは何か」を視覚的に示す役割も担っています。
箱の大きさを見ればデータのばらつきが、ひげの長さを見れば全体の広がりが直感的にわかります。
箱ひげ図の意味と必要性
箱ひげ図の「意味」と「必要性」についても具体的に見てみましょう。
- 意味
箱ひげ図とは、データの分布を視覚的に理解するためのグラフです。
四分位範囲・中央値・最小値・最大値を1つの図にまとめることで、データの特徴を瞬時に把握できます。 - 必要性
箱ひげ図の必要性は、複数のデータを比較する場面で特に強く現れます。
例えば、異なる2つのクラスのテスト結果を比べるとき、平均点だけを見ても差は小さいかもしれません。
しかし、箱ひげ図を並べれば、「どちらのクラスの点数が安定しているか」「どちらのクラスに外れ値があるか」などがひと目で理解できます。
また、箱ひげ図は学校の学習だけでなく、企業の品質管理や医療研究のデータ比較など、社会のあらゆる分野で使われています。
そのため、中学生の段階で「箱ひげ図の意味」や「箱ひげ図の必要性」を理解しておくことは、将来に向けて大きな価値があるのです。
四分位範囲の求め方と計算例

ここまでは「四分位範囲とは何か」「箱ひげ図とは何か」といった基本的な意味や必要性について解説しました。
ここからはさらに一歩踏み込み、実際に四分位範囲を求める方法や、箱ひげ図を描く手順を学んでいきます。
具体例を通して理解を深めることで、単なる暗記ではなく実践的な知識として活用できるようになります。
四分位範囲を理解するには、実際にデータを並べて計算してみるのが一番です。
ここでは、まず中学2年生が身近に感じられる「テストの点数」を題材にして考えてみましょう。
例題1:テストの点数
あるクラスで行われた数学の小テストの点数を、小さい順に並べると次のようになりました。
このデータをもとに四分位範囲を求めます。
- 中央値(Q2)を求める
データの数は11個なので、6番目の値が中央値です。
Q2 = 60 - 第1四分位数(Q1)を求める
下位のデータ(35, 40, 45, 50, 55)の中央値を取ります。
中央値は45です。
Q1 = 45 - 第3四分位数(Q3)を求める
上位のデータ(65, 70, 75, 80, 85)の中央値を取ります。
中央値は75です。
Q3 = 75 - 四分位範囲を計算する
四分位範囲 = Q3 – Q1 = 75 – 45 = 30
つまり、このデータの四分位範囲は30点となります。
四分位範囲の解釈
ここで求めた「四分位範囲=30点」にはどんな意味があるのでしょうか。
- 意味
データの真ん中50%の人たちは、45点から75点の間に分布していることを意味します。 - 必要性
平均点(この場合は約60点)だけでは、「どれくらいの人が平均点付近にいるのか」がわかりません。しかし四分位範囲を見れば、「大半の生徒が45点~75点に収まっている」とすぐにわかり、学習状況をより的確に把握できます。
このように、「四分位範囲とはデータの真ん中部分を示すものであり、外れ値に左右されにくく全体像をとらえるのに役立つ」という点が再確認できます。
箱ひげ図の描き方と例

次に、四分位範囲をもとに「箱ひげ図」を描いてみましょう。
箱ひげ図の描く手順
- データを小さい順に並べる
- 最小値、Q1、中央値(Q2)、Q3、最大値を求める
- Q1~Q3の範囲を「箱」として描き、その中に中央値を線で記す
- 最小値と最大値を「ひげ」として描き加える
例題2:先ほどのデータを箱ひげ図にする
データ
求めた数値は次の通り
- 最小値 = 35
- Q1 = 45
- Q2 = 60
- Q3 = 75
- 最大値 = 85
これを箱ひげ図にすると、次のようなイメージになります。
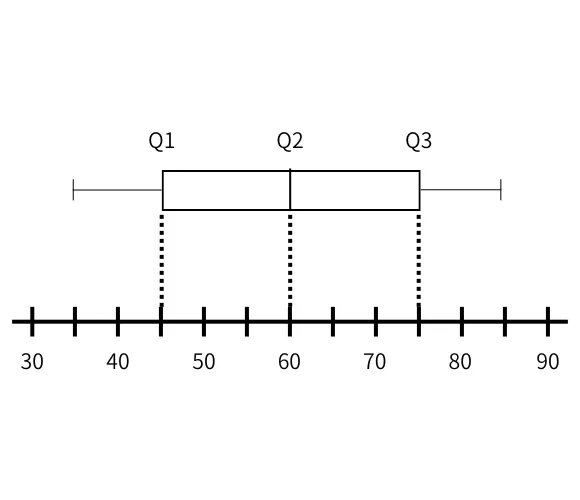
ここで、四角い部分(45~75)が「箱」にあたり、その中の線が中央値(60)を示します。
そして、左右に伸びる線が「ひげ」となり、データ全体の広がりを表します。
箱ひげ図から読み取れること
この箱ひげ図からは、以下のような特徴が読み取れます。
- 真ん中50%の生徒(半分)は、45点から75点の間にいる。
- 成績の広がりは35点から85点までで、ばらつきが大きすぎるわけではない。
- 中央値が箱の真ん中にあるので、点数の分布は比較的バランスが取れている。
つまり、箱ひげ図とは「四分位範囲の意味を直感的に理解できる図」であり、データの比較や分析にとても役立つのです。
複数のデータを比較する実例

箱ひげ図や四分位範囲の真価は、「複数のデータを比較するとき」に発揮されます。
例題3:2つのクラスのテスト結果を比較
- Aクラスのテスト結果(四分位範囲=30)
- Bクラスのテスト結果(四分位範囲=15)
両クラスの平均点は同じ60点だったとします。
しかし、四分位範囲を見ると違いが明らかになります。
- Aクラスは45~75点の幅に生徒が分布 → ばらつきが大きい
- Bクラスは52.5~67.5点の幅に集中 → 成績が安定している
箱ひげ図で並べれば、Bクラスの方が成績がまとまっていることがひと目でわかります。
学校以外での応用例
このような比較の仕方は、学校だけでなく社会のさまざまな場面でも使われます。
- 企業の品質管理
製品の長さや重さにばらつきがあるかを確認する際に箱ひげ図を用いる。 - スポーツ分析
選手の記録の安定性を比較するために四分位範囲を活用。 - 医療研究
患者の治療効果や副作用の分布を比較する際に箱ひげ図を使う。
このように、「箱ひげ図の意味」や「四分位範囲の必要性」は学校の勉強を超えて、社会での実際のデータ活用に直結しています。
社会における四分位範囲の意味と必要性

ここまでの説明では「四分位範囲とは何か」「箱ひげ図とは何か」といった基礎を学び、計算の方法や描き方を実際のデータを用いて確認しました。
それらを踏まえてここからはさらに一歩進んで、これらの知識が社会でどのように役立つのか、また今後の学びや生活にどうつながるのかを考えていきましょう。
数学の学習内容は一見すると「テストのためだけ」と思われがちですが、実は社会のさまざまな分野で直接活用されています。
特に「四分位範囲」と「箱ひげ図」は、データ分析や比較に欠かせない道具です。
四分位範囲が役立つ場面
- 教育現場
学校でクラス全体のテスト結果を分析するときに、単なる平均点だけでは実態がわかりません。
四分位範囲を調べれば、学力のばらつきが大きいのか小さいのかがわかり、授業の改善や補習計画に役立ちます。 - 企業の品質管理
製品のサイズや重さにばらつきがある場合、平均だけを見ると正しく評価できないことがあります。
四分位範囲を調べれば「大半の製品が基準内に収まっているかどうか」を確認でき、不良品の割合を把握できます。 - スポーツの記録分析
選手のタイムやスコアを評価するとき、最高記録や平均だけでは実力が安定しているかどうかは判断できません。
四分位範囲が小さいほど安定した成績を出していることを意味し、選手の強みを客観的に示せます。 - 金融や投資のリスク評価
株価や投資信託の収益率は大きく変動することがあります。
平均的な利益率だけで判断すると危険ですが、四分位範囲を調べれば「利益率のばらつき=リスクの大きさ」をより正確に把握できます。
このように、四分位範囲の意味は単なる「計算問題の答え」ではなく、データの本質を捉えるための重要な指標であることがわかります。
四分位範囲を理解することの将来への価値
「四分位範囲とは何か」を理解しておくことは、中学生にとって将来の学びや仕事に直結します。
- 高校や大学で学ぶ統計学やデータ分析の基礎になる。
- 将来どんな職業に就いても、データを扱う場面で「平均だけでなく分布を意識する」習慣が役立つ。
- 情報社会で必要とされる「批判的にデータを見る力」を養える。
つまり、四分位範囲の必要性は、単なる数学の一部にとどまらず、「データ社会を生きるための基礎力」にあるのです。
社会における箱ひげ図の意味と必要性

箱ひげ図は、複数のデータを比較する際に非常に有効です。
ひと目でデータの全体像を把握できるため、教育、ビジネス、医療、研究など幅広い分野で利用されています。
箱ひげ図が役立つ場面
- 教育現場での比較
2つのクラスや学年のテスト結果を比較する際、平均点ではなく箱ひげ図を並べることで「どちらのクラスが安定しているか」「外れ値が多いか」などを視覚的に把握できます。 - 医療分野の研究
治療法ごとの効果を比較するとき、患者の改善度合いを箱ひげ図で表せば、効果が安定している治療と個人差が大きい治療を区別できます。 - ビジネスの売上比較
店舗ごとの売上データを箱ひげ図で比較すれば、「ある店舗は売上の幅が大きく波がある」「別の店舗は安定している」といった特徴が明らかになります。 - 社会調査や世論調査
アンケート結果を分析する際に箱ひげ図を用いると、単なる平均や最頻値では見えない「回答の広がり」や「多数派と少数派の位置関係」が把握できます。
箱ひげ図の強みと必要性
箱ひげ図とは、数値をそのまま列挙するのではなく、データのまとまりやばらつきを図で表す点に大きな意味があります。
- 視覚的にわかりやすい
数字の表を見ただけではわかりにくい特徴が、箱ひげ図にすると直感的に理解できます。 - 複数のデータを一度に比較できる
2つ以上のグループを比較するとき、平均点の差だけでなく「データのばらつき」や「中央値の位置」を同時に確認できます。 - 外れ値を見つけやすい
極端に高い値や低い値があった場合、箱ひげ図のひげから飛び出して表示されるので、外れ値がすぐに見つかります。
このように、箱ひげ図の必要性は「公平かつ効率的にデータを比較できること」にあります。
データリテラシーと日常生活への応用

現代社会では「データを正しく読み取る力=データリテラシー」がますます重要になっています。
インターネットやニュースでは毎日のように統計や調査結果が報道されますが、平均だけを見て誤解することも少なくありません。
日常生活での例
- ニュース記事を読むとき
「平均年収○○万円」という報道を目にすることがあります。
しかし、四分位範囲や箱ひげ図を用いて分布を確認すると、実際には大きな格差があることがわかる場合があります。 - 健康情報を判断するとき
「平均体重」や「平均睡眠時間」だけでなく、どの範囲に多くの人が含まれているのかを見られると、自分がどの位置にいるかを正しく判断できます。 - 買い物やレビューを確認するとき
商品のレビュー評価が「平均★4.0」だったとしても、実際には「★5が多いが★1も多い」のか、「★4ばかりで安定している」のかで意味は大きく異なります。
箱ひげ図をイメージすれば、その違いを考えられるようになります。
将来の仕事における活用
- 研究者や技術者
データのばらつきを分析し、新しい発見や改善策を導き出す。 - ビジネスマン
売上や顧客満足度を比較し、戦略を立てる。 - 医師や看護師
治療効果や検査結果の分布を理解し、患者に合わせた対応をする。 - 行政や政策立案者
社会調査の結果を分析し、より公平で効果的な政策を考える。
どの職業でも「平均値だけでなく、データの分布をどう理解するか」が重要であり、そこで四分位範囲や箱ひげ図の知識が活かされるのです。
まとめ
中学2年で学習する「データの分布」は、統計の学びの中でも特に重要な単元です。
数値をただ並べて見るのではなく、データ全体の特徴を客観的に把握し、比較や判断に活かす力を育てます。
特に「四分位範囲とは何か」を理解することで、データの散らばり具合やバラつきを具体的に表現できるようになります。
単に平均や中央値だけでなく、「どのくらいの幅にデータがまとまっているのか」という情報が加わることで、データの意味がより深く理解できるのです。
これは「四分位範囲の意味」や「四分位範囲の必要性」を学ぶ上で非常に大切なポイントです。
さらに「箱ひげ図とは何か」を学ぶことで、数値だけでは分かりにくいデータの特徴を一目で可視化できる力を得られます。
箱ひげ図は「中央値」「四分位数」「外れ値」を同時に示せるため、比較やプレゼンテーションの場でも役立ちます。
こうした点から、「箱ひげ図の意味」や「箱ひげ図の必要性」は、将来の社会生活や仕事に直結する重要な知識となります。
このページで学習したどの場面でも共通するのは、データを「正しく理解し、伝え、比較できること」こそが統計の力だということです。
学生さんが学ぶ「データの分布」は、ただの数学の知識にとどまりません。
買い物やスポーツ成績の分析から、将来のビジネスや研究活動に至るまで、幅広い場面で活用される「一生使える道具」です。
ぜひ今回学んだ「四分位範囲」や「箱ひげ図」の考え方をしっかり身につけ、自分の生活や未来に役立てていきましょう。










コメント