中学校2年生で学習する「平行線や角の性質」は、数学の図形分野の基礎を理解するうえで欠かせない内容です。
これらの性質は、三角形や四角形の角度を求める問題に直結するだけでなく、高校数学の図形や証明問題、さらには理科や物理で角度を使った計算を行う際の基盤ともなります。
特に「同側内角」「三角形の内角の和」「三角形の外角の和」といった知識は、入試問題や実生活の場面でも活用できる重要なテーマです。
なので、ここではまず同側内角とは何かを深く解説します。
そして、そこから三角形の角度計算へとつながる流れを理解できるように構成していきます。
中学生が混乱しやすいポイントも補足しながら、基礎から丁寧に説明していきましょう。
同側内角とは何か?

まず、同側内角ということはについて見ていきます。
同側内角とは、横切線の同じ側にあり、かつ平行線の内側にある2つの角のことをいいます。
例えば、横切線を境にして右側にできた2つの内側の角が同側内角です。
このとき、平行線であれば同側内角の和は180°になるという性質が成り立ちます。
これは非常に重要な性質で、後に三角形の内角の和や外角の和を考えるときの基盤となる考え方です。
言葉だけの説明では少々分かりにくい部分もあるので、図で表してみます。
上記の定義を図示すると、下記の図のようになります。
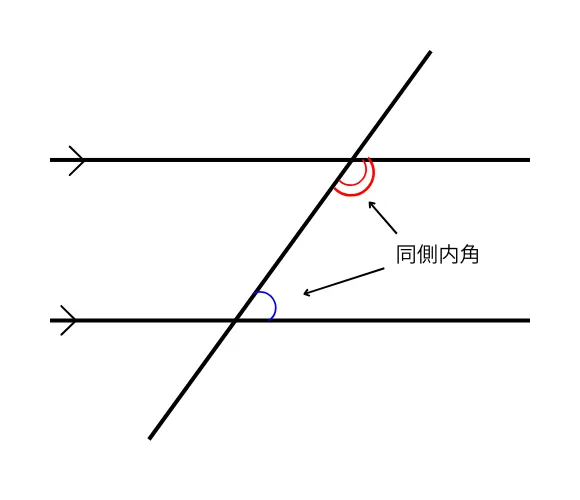
同側内角の性質を詳しく理解する

ここまでで、同側内角の位置関係と定義は確認できました。
では、なぜ同側内角の和が180°になるのかを考えてみましょう。
同側内角の和はなぜ180°になるのか?
上図を改めて見てみましょう。
2本の平行線を引き、それを横切る直線を1本加えます。
このとき、同側内角を取り出してみると、1つの角と隣の角がちょうど「一直線をはさんだ角の関係」になっています。
1本の直線にできる角の和は180°になるため、同側内角を足すと必ず180°になるのです。
実際の例で確認してみよう
例えば、ある同側内角の一方が110°だったとします。
このとき、もう一方の同側内角は必ず70°になります。
なぜなら、110°+70°=180°だからです。
この関係を使えば、平行線と角の問題を解くときに「残りの角をすぐに求める」ことができます。
入試問題では、与えられた角度から次々と角度を計算していく問題が多いので、この性質をきちんと理解しておくことが大切です。
同側内角の性質を利用した問題
これらの知識を押さえたうえで、実際の問題を見てみましょう。
例題
平行線$l$と$m$ があり、それを直線$n$が横切っているとします。$n$と$l$の交点でできた角が65°でした。このとき、同側内角にあたる角の大きさを求めなさい。
解き方
同側内角の和は180°なので、180°-65°=115°。
よって、もう一方の角は115°になります。
三角形の内角の和につながる考え方

同側内角の性質を理解すると、次に学ぶ「三角形の内角の和」への橋渡しがしやすくなります。
三角形の角度に関する性質も、実は平行線を使った考え方で説明できるのです。
三角形の内角の和を導く方法
三角形の内角の和が180°であることは有名ですが、この証明にも平行線と同側内角の性質が関わっています。
三角形の1つの辺を延長し、その反対側にその辺と平行な線を引くと、三角形の他の2つの角が同側内角として現れます。
この2つの角の和は180°から1つの角を引いたものになるので、結局、三角形の3つの角の和が180°であることが分かるのです。
証明をわかりやすく整理する
上記の証明の内容をもう少し分かりやすく考えてみたいと思います。
三角形ABCを考えます。
辺BCを延長し、その点Aを通る直線をBCに平行に引きます。
すると、$\angle A$の両隣にある角は、それぞれ三角形の角Bと角Cに等しくなります。
したがって、$\angle A+\angle B+\angle C=180°$となり、三角形の内角の和は180°であることが示されます。
三角形の内角の和を深く理解する

ここまでは、平行線と角の関係から「同側内角とは何か」を確認し、そこから「三角形の内角の和」へつながる考え方を紹介しました。
ここからは、三角形の内角の和をより体系的に理解すること、そして新たに重要な性質である三角形の外角の和について解説していきます。
これらは教科書に必ず登場する大切なテーマであり、証明問題・応用問題の基礎になる考え方です。
さらに、「なぜそうなるのか」を視覚的に理解できるように図形のイメージを使って説明し、具体的な例題や入試レベルの活用問題も交えながら整理していきます。
では、まず三角形の内角の和についてもう少し深堀していくことから行っていきます。
三角形の内角の和が180°であることは、数学を学ぶ上で最初に出会う「図形の不変の法則」といえます。
多くの中学生が最初は暗記として受け止めがちですが、平行線の性質を使って導けるという点が重要です。
直感的な理解の仕方
平行線を使って180°を証明する方法は上記で説明した通りですが、より直感的に180°をイメージする方法もお伝えしておきます。
三角形を紙で作り、その3つの角を切り取って並べてみるとどうなるでしょうか。
実際に角を合わせると、3つの角をぴったり並べると一直線(180°)になることがわかります。
これは視覚的に三角形の内角の和が180°であることを実感できる方法です。
数学の抽象的な証明だけでなく、こうした直感的な確認をしておくと、より理解が深まります。
三角形の内角の和を利用した問題
では実際に三角形の内角の和を利用した問題も見ていきましょう。
例題
三角形の2つの角がそれぞれ50°と70°であるとき、残りの角を求めなさい。
解き方
三角形の内角の和は180°なので、180°-(50°+70°)=60°。
よって、残りの角は60°になります。
入試では、角度が直接与えられるだけでなく、「平行線を使った補助線を引いて求める」などの応用問題が多いため、内角の和の性質は必ず使えるようにしておきましょう。
三角形の外角の和とは何か?

三角形に関するもう一つの重要な性質が「外角の和」です。
多くの中学生が最初は戸惑いやすい部分ですが、これも非常にシンプルで強力な性質を持っています。
三角形の外角の和は360°になる
三角形の外角とは、三角形の各頂点で辺を延長したときにできる角のことです。
例えば、$\angle A$に接する辺を延長すると、その外側にできる角を「$\angle A$の外角」といいます。
三角形には3つの頂点があるため、外角も3つできます。
このとき、三角形の外角の和は必ず360°になるという性質が成り立ちます。
この性質は、三角形の内角の和が180°になるのと同じように、知識としてしっかりと定着させてください。
なぜ外角の和は360°になるのか?
外角の和を理解するために、三角形ABCを例に考えてみましょう。
外角は、内角と「180°の差」として表せます。
つまり、外角A=$180°-\angle A$、外角B=$180°-\angle B$、外角C=$180°-\angle C$です。
これらをすべて足し合わせると、
外角A+外角B+外角C=$(180°-\angle A)+(180°-\angle B)+(180°-\angle C)$
=$540°-(\angle A+\angle B+\angle C)$。
ここで、三角形の内角の和=180°であることを思い出すと、
外角A+外角B+外角C=540°-180°=360°。
したがって、三角形の外角の和は常に360°になるのです。
三角形の外角の性質を利用した考え方
外角の性質でもう1つ重要な性質があり、それは三角形の1つの外角は、他の2つの内角の和に等しいということです。
例えば、三角形ABCの$\angle A$の外角は、$\angle B+\angle C$と等しくなります。
これは入試問題で非常に頻出する性質です。
内角の和と外角の和を結びつけて理解する

ここまでで、三角形の内角の和=180°、外角の和=360°という2つの性質を確認しました。
実は、この2つの性質は表裏一体の関係にあります。
内角と外角の関係を整理する
- 内角の和=180°
- 外角の和=360°
- 1つの外角=残り2つの内角の和
この3つをあわせて理解しておくことで、応用問題を解くときに迷わず進められます。
特に、「補助線を引くときに外角を利用する」といった場面では、この関係をスムーズに思い出せるかが重要です。
例題で確認する
例題
三角形の1つの外角が120°であるとき、その隣接する内角を求めなさい。
解き方
外角と内角は180°の差なので、180°-120°=60°。
例題2
三角形のある外角が130°である。この三角形の残りの2つの内角の和を求めよ。
解き方
1つの外角は、残りの2つの内角の和に等しい。
したがって、答えは130°となる。
三角形の性質を活用した応用問題

内角の和や外角の和を理解したら、実際に問題に応用していきましょう。
ここでは中学2年生がよく出会うレベルの問題をいくつか紹介します。
角度を組み合わせて求める
問題
三角形の2つの外角がそれぞれ120°、110°であるとき、残りの外角を求めなさい。
解き方
外角の和は360°なので、残りの外角=360°-(120°+110°)=130°。
補助線を使った角度計算
問題
三角形ABCにおいて、$\angle A=50°$、$\angle B=60°$のとき、辺BCを延長してできる外角を求めよ。
解き方
三角形の内角の和=180°なので、$\angle C=70°$。
辺BCを延長してできる角Cの外角は180°-70°=110°。
入試レベルの活用
入試では「三角形や四角形に補助線を引いて、外角を利用して解く」問題がよく出題されます。
例えば、台形や平行四辺形の角度を求める問題では、三角形の外角の性質を利用すると計算が簡単になることがあります。
平行線や三角形の性質が日常生活で役立つ場面

ここまでで「平行線と角の性質」や「同側内角とは何か」を確認し、「三角形の内角の和」「三角形の外角の和」について学びました。
それらの知識を踏まえて、ここからは、これらの性質が日常生活や入試、そして将来の学習にどのように役立つのかを具体的に見ていきましょう。
単なる暗記で終わらせるのではなく、「なぜ必要か」「どのように活かされるか」まで理解することで、学習のモチベーションが高まり、より確かな知識となります。
まずは日常生活で活かされている例を見ていきます。
数学の学習では「これを覚えて何に使うの?」という疑問を持つ人も多いと思います。
しかし、平行線や角の性質、三角形の角度に関するルールは、実際の生活や仕事の中でさまざまな場面に応用されています。
建築やデザインの中での活用
建築物や橋を設計するとき、三角形の性質は強度計算に欠かせません。
たとえば、屋根の骨組みや鉄塔の設計では、三角形の内角や外角の性質を利用して正確な角度を決定します。
もし三角形の内角の和が180°でなければ、建築物の安定性は大きく損なわれてしまうでしょう。
地図や測量での利用
測量士が土地の面積を計算するときにも、三角形の性質は欠かせません。
実際の土地を小さな三角形に分け、その角度を測って計算する方法が一般的です。
三角形の内角の和や外角の性質を知っていると、誤差を減らしながら効率的に測量を進めることができます。
身近な生活の中の三角形
スポーツでも三角形の性質は役立ちます。
サッカーでゴール前に三角形のパスコースを作る、バスケットボールでトライアングルオフェンスを組むなど、「角度の取り方」を意識することでプレーの幅が広がります。
これは「三角形の角度の関係を理解すること」が戦術にも通じる例です。
入試に向けての活用と学習法

中学数学では、平行線や三角形の性質を使った角度の問題が頻出です。
ここからは、入試に向けて効率よく学習するためのポイントを整理します。
角度問題を解くときの流れ
角度の問題を解くときには、次の手順を意識するとスムーズです。
- 補助線を引く ― 平行線を作るように補助線を引き、同位角・錯角を見つける。
- 同側内角を利用する ― 2つの角の和が180°になる関係を使う。
- 三角形の内角の和を使う ― 3つの角の和が180°であることから残りの角を求める。
- 外角の性質を利用する ― 外角=残りの2つの内角の和を使う。
この4つのステップを押さえれば、ほとんどの角度問題に対応できます。
よくある間違いと対策
三角形の性質を利用した問題において、よくある間違いとその対策についても紹介します。
- 同側内角を錯角と混同する
→ 図に色をつけて位置関係を整理すると理解しやすいです。 - 外角を「内角の補角」とだけ覚えてしまう
→ 外角=他の2つの内角の和、という性質も必ず押さえましょう。 - 計算だけで解こうとする
→ 図形問題では、補助線を引く直感を鍛えることが大切です。
入試問題での出題パターン
入試では、次のようなパターンで出題されることが多いです。
- 平行線を利用して角度を求める
- 三角形の外角を利用した応用問題
- 四角形や多角形に発展して「内角の和」を使わせる問題
- 証明問題(「$\angle A=\angle B$であることを証明せよ」など)
これらはすべて今回学んだ性質の延長にあります。
将来につながる学びとしての平行線と角の性質

数学の学習は入試だけのためではありません。
平行線や三角形の性質は、高校数学やその先の分野でも大きな役割を果たします。
最後にその例もいくつか紹介しておきます。
高校数学での発展
高校に進むと、ベクトルや三角比を学ぶ際に、角度の性質が再び登場します。
例えば、三角比の定義では直角三角形の内角や外角の関係を利用しますし、ベクトルの計算では角度の成す関係が重要です。
理科や物理への応用
理科の光の反射や屈折の学習では、角度の性質を正しく理解しているかが問われます。
特に「入射角=反射角」というルールも、平行線や角の性質を基礎として理解できます。
社会や仕事で役立つ場面
将来、建築、測量、デザイン、エンジニアリングなど、角度や図形を扱う分野に進む場合、この基礎知識は必ず活かされます。
つまり、「今の学習は将来の可能性につながる投資」でもあるのです。
まとめ
このページでは、同側内角の定義から始まり、三角形の内角の和の性質と外角の和の性質、内閣と外角の関係性について解説を行ってきました。
改めてここで学んだことをまとめると、
- 同側内角とは何か:横切線と平行線でできる内側の角で、和は180°になる。
- 三角形の内角の和:必ず180°になる。
- 三角形の外角の和:必ず360°になる。
- 1つの外角=残り2つの内角の和。
- これらは入試や実生活、高校数学や仕事にもつながる重要な知識である。
このように、平行線や角の性質は単なる暗記で終わらせず、実際の問題や生活にどうつながるかを意識すると、学びの価値が一層深まります。
三角形については最も基本的な平面図形であり、問題の出題方法も無数にあります。
このページで学んだ知識をしっかりと定着させて、どのような問題でも対応ができるように学習を続けていきましょう。










コメント