中学2年で学ぶ「平行線と角の性質」は、図形の基礎を理解する上でとても重要な単元です。
特に「同位角」「対頂角」「錯角」という角度の種類は、平行線の特徴を理解するために欠かせないものです。
これらの性質をしっかり身につけることで、数学の問題を解くだけでなく、将来の実生活や科学技術の世界でも役立つ知識になります。
ここでは、平行線や角の性質について、丁寧に解説していきます。
まずは、基本的な角の種類や性質を一つひとつ整理しながら学んでいきましょう。
平行線と角の性質を学ぶ意味

中学校の数学で平行線や角の性質を学ぶ理由は、単なる知識の暗記ではありません。
図形の世界には必ず「規則性」や「法則」が存在します。
これを理解することで、複雑な図形の問題でも筋道を立てて考えられるようになります。
例えば、街の建物の設計図や地図、道路の交差点など、私たちの生活の中には「平行」や「角の関係」が数多く登場します。
建築士が設計を行うときも、測量士が土地を測るときも、必ずこの「平行線と角の性質」を正しく理解していなければ成り立ちません。
そのため、この単元は単なる学校のテスト対策を超えた「実用性のある数学」と言えるのです。
平行線と角の関係を理解する第一歩

まず、平行線の定義を確認しておきましょう。
平行線とは「同じ平面上にあって、どこまで延長しても交わらない2つの直線」のことをいいます。
この平行線に1本の直線(これを横切線と呼びます)が交わると、多くの角が生まれます。
これらの角の中で特に注目すべきものが「同位角」「錯角」「対頂角」です。
これら3種類の角の性質を理解することは、中学数学だけでなく、高校数学で登場する「図形と証明」や「三角比」の学習の基盤になります。
平行線に関わる角の種類を整理する

平行線を横切る直線があると、図形の中にはいくつもの角ができます。
その中で重要な関係を持つのが次の3つです。
- 同位角
- 錯角
- 対頂角
この3つは一見似ているように見えますが、それぞれ異なる場所にあり、異なる性質を持っています。
以下では、それぞれの種類について詳しく見ていきましょう。
同位角とは何か

平行線の学習で最初に登場するのが「同位角」です。
同位角の定義と位置関係
同位角とは、平行線とそれを横切る直線がつくる角のうち、同じ位置にある角のことを指します。
たとえば、上下の平行線を横切る1本の直線を考えたとき、左上にできた角と左下にできた角が「同位角」になります。
「同じ位置」というのは、平行線のそれぞれの交点にできる4つの角の中で、対応する場所にある角を意味します。
同位角の性質
平行線が成り立っている場合、同位角は必ず等しくなるという性質があります。
つまり、平行線における同位角は常に「角度が同じ」になるのです。
この性質は、問題を解くときに大きな武器となります。
例えば、ある角度が60°とわかっていれば、それと同位角の角度も60°であるとすぐに判断できます。
同位角の活用例
実生活でも、同位角の考え方はよく使われています。
道路の横断歩道の白線や、ビルの窓枠が等しい間隔で並んでいるとき、その延長線を考えると平行線と同位角の関係を発見できます。
建築設計においても、同位角の一致が建物の水平や垂直を正しく保つことに繋がっているのです。
錯角とは何か

次に学ぶのが「錯角」です。
錯角の定義と位置関係
錯角とは、平行線と横切線がつくる角のうち、交わる位置が対角線上にある角のことです。
具体的には、上側の平行線の右側にある角と、下側の平行線の左側にある角が「錯角」の関係になります。
「錯」という言葉は「交差している」ことを意味しており、その名のとおり平行線と横切線がつくる図形の中で斜めに対応している角を指します。
錯角の性質
平行線である場合、錯角は必ず等しいという性質があります。
これは同位角と同じく、平行線に横切線が交わるときの基本法則です。
この性質を利用すると、錯角を使って他の角の大きさを求めたり、図形が本当に平行であるかどうかを確かめることができます。
錯角の活用例
地図を見ているとき、道路が交差している場所に平行な道路が引かれていると、その角度を計算する際に錯角の関係が使えます。
また、機械設計やロボット工学でも、斜めに交わる部品が平行性を保つために錯角の原理が応用されています。
対頂角とは何か

最後に紹介するのが「対頂角」です。
対頂角の定義と位置関係
対頂角とは、2本の直線が交わるとき、その交点を挟んで向かい合う角のことをいいます。
たとえば、道路の交差点を真上から見たとき、交差する道路がつくる角の向かい合った2つの角が対頂角です。
対頂角の性質
対頂角には大きさが常に等しいという性質があります。
これは平行線がなくても成り立つ、直線そのものの性質です。
つまり、交わる2本の直線があれば、必ず対頂角は等しい角度を持つことになります。
対頂角の活用例
対頂角は、道路の交差点や、建物の柱の配置を考えるときによく登場します。
また、幾何学的な証明問題を解くときにも欠かせない性質であり、論理的に角度の等しさを示す際の出発点となります。
これらの角を1つの図でまとめてみると下記のような図になります。
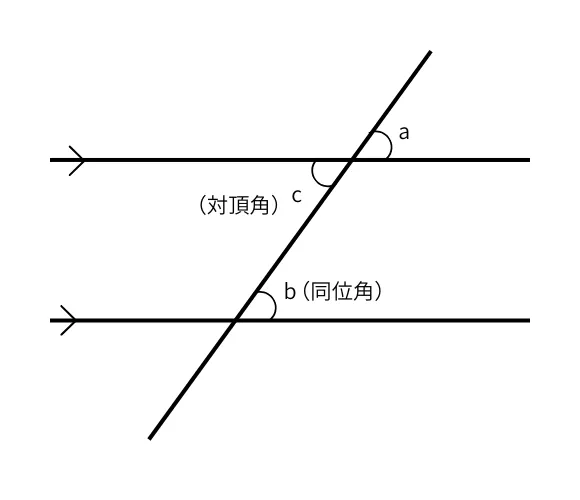
$\angle a$に対して、
- $\angle b$が同位角
- $\angle c$が対頂角
になります。
また、
$\angle b$と$\angle c$は錯角
そして、
$\angle a = \angle b = \angle c$
という関係になっています。
ここまでは、平行線に関連する「同位角」「錯角」「対頂角」の基本的な定義と性質を整理しました。
ここからは、それらを実際に使ってどのように問題を解いていくのかを具体的に見ていきましょう。
この段階では、単なる知識の暗記ではなく、「なぜその角が等しくなるのか」「どの性質を使えば角度を求められるのか」といった論理的な思考を大切にすることが重要です。
これを意識することで、平行線の角に関する問題が一気に解きやすくなります。
同位角を利用した問題の解き方

同位角は平行線に横切線が交わるときに現れる関係で、もっとも基本的でわかりやすい性質です。
典型的な問題例
問題
平行線ABとCDに横切線EFが交わっている。$\angle x = 70°$のとき、対応する同位角の大きさを求めなさい。
解き方
- 平行線であることから、同位角は等しい性質を持つ。
- よって、求める角度も70°になる。
このように、同位角を利用すると「与えられた角度と等しい角度をすぐに見つけられる」ため、問題の処理がスムーズに進みます。
応用問題
問題
平行線ABとCDに横切線EFが交わっている。$\angle a =110°$のとき、同位角と錯角の大きさをすべて求めなさい。
解き方
- 同位角 → $\angle a =110°$なので、その同位角も110°。
- 錯角 → 平行線であるため、錯角も110°。
こうして同位角から出発すると、図形全体の角度が次々と求まることがわかります。
錯角を利用した問題の解き方

錯角は斜めに位置する角で、最初は少し見つけにくいですが、平行線が与えられているときに非常に重要な手がかりとなります。
典型的な問題例
問題
平行線ABとCDに横切線EFが交わっている。$\angle p = 65°$のとき、錯角の大きさを求めなさい。
解き方
- 平行線であるため、錯角は等しい。
- よって、求める角度も65°。
このように、錯角の性質を使うと簡単に角度を特定できます。
発展的な使い方
問題
平行線ABとCDに横切線EFが交わっている。$\angle p = 120°$のとき、その他の角度をすべて求めなさい。
解き方
- 錯角の関係を使い、もう一方の錯角も120°とわかる。
- 同位角の性質を使えば、同位角も120°。
- 対頂角の性質を使えば、反対側の角も120°。
- 残りの角は関係は直線(=180°)から120°を引くと、60°
このように、錯角を起点にして同位角・対頂角を組み合わせると、図形全体の角度を完全に把握できます。
対頂角を利用した問題の解き方

対頂角は平行線がなくても成り立つ性質ですが、平行線の問題でもしばしば登場します。
典型的な問題例
問題
2本の直線が交わって$\angle x =85°$ができた。このとき、対頂角の大きさを求めなさい。
解き方
- 対頂角は常に等しい性質を持つ。
- よって、$\angle x = 85°$の対頂角も85°となる。
この性質はシンプルですが、証明問題などでよく使われる基本ルールです。
平行線と組み合わせる
問題
平行線ABとCDに横切線EFが交わっている。$\angle y = 100°$のとき、対頂角と同位角、錯角の関係を整理しなさい。
解き方
- $\angle y = 100°$→ その対頂角も100°。
- さらに平行線の同位角・錯角の関係を使うと、同じく100°の角が複数現れる。
このように、対頂角は単独でも有効ですが、平行線の性質と組み合わせることでより強力になります。
角の性質を使った証明問題の考え方

ここまでの内容を理解したうえで、中学2年の図形学習で避けて通れないのが「証明問題」です。
角の性質を理解したら、それを論理的に説明する力を養う必要があります。
証明問題の基本手順
証明問題を解くときは、次の手順で考えます。
- 与えられた条件を整理する
例:「$AB /\!/ CD$」「$\angle x = \angle y$を証明せよ」など。 - 使える性質を探す
同位角・錯角・対頂角のいずれかを適用できるか考える。 - 論理の流れを作る
「$AB /\!/ CD$だから、同位角が等しい」など、理由をはっきり書く。 - 結論を導く
「したがって$\angle x = \angle y$」とまとめる。
例題で確認
問題
平行線ABとCDに横切線EFが交わっている。$\angle a$と$\angle b$が錯角の位置にあるとき、$\angle a = \angle b$であることを証明しなさい。
解答
- $AB /\!/ CD$が与えられている。
- 平行線と横切線の性質から、錯角は等しい。
- よって、$\angle a = \angle b$。
このように、証明問題では「なぜ等しいのか」を性質に基づいて説明することが求められます。
角の性質を使いこなすコツ

ここまで見てきたように、「同位角」「錯角」「対頂角」は、それぞれ単独でも強力な性質を持ちますが、組み合わせることでより複雑な問題も解けるようになります。
性質の見極め方
- まず「平行線があるかどうか」を確認する。
- 平行線があるなら「同位角」や「錯角」を考える。
- 平行線がなくても直線が交わっていれば「対頂角」を考える。
このように、「図を見たらまず性質を分類する」という意識が大切です。
論理的思考の練習
また、ただ答えを求めるのではなく、どの性質を使ったのかを説明する練習を繰り返すと、証明問題にも強くなります。
さらに、将来の数学や理科の学習でも「なぜそうなるのか」を説明できる力は非常に重要です。
日常生活に活きる平行線と角の性質

ここまでで、平行線と角の性質、特に同位角・錯角・対頂角の種類と特徴を詳しく解説しました。
ですが知識としては理解できても、「それが実際の生活でどのように活きるのか」「将来、どんな場面で必要になるのか」と疑問を持つ人も多いでしょう。
実は、これらの角の性質は単なる学校の勉強ではなく、建築・測量・デザイン・エンジニアリングなど、私たちの暮らしや社会の基盤を支える重要な知識なのです。
ここからは、平行線や角の性質が具体的にどのように役立っているのかを掘り下げて解説していきます。
角の性質は、私たちが普段意識せずに触れている場面にたくさん登場します。
街の中に潜む同位角
例えば、大通りと横道が交わる交差点を思い浮かべてください。
大通りの両側の歩道は平行に作られています。
その平行な歩道を横切る形で横断歩道が設置されると、交差点の角度の中に「同位角」が現れます。
もし設計の段階で歩道がわずかに平行でなかったとしたら、横断歩道の白線が不揃いになったり、建物の配置に歪みが出たりします。
同位角が等しいという性質は、都市計画や道路設計に欠かせない考え方なのです。
建物や家具に隠れた錯角
家の中でも錯角の性質を見つけることができます。
例えば、床と天井は平行であり、そこに斜めに梁(はり)が通っている場合、その梁と床・天井が作る角度の中には錯角が存在します。
この錯角が等しくなることは、建物全体の安定性を保つために重要です。
もし錯角が狂ってしまうと、家が傾いたり歪んだりする原因になります。
日常の中の対頂角
道路の交差点に立ったとき、信号機の柱や電柱などが交わる部分を観察すると、対頂角が自然に現れています。
対頂角が等しいという性質は、設計の正確さを確認する上でとても役立ちます。
例えば工事現場では、直線が正しく交わっているかどうかを確認する際に対頂角を測定することがあります。
スポーツや趣味に生かされる角の性質

角度の性質は勉強の場だけでなく、スポーツや趣味の中でも活躍しています。
サッカーやバスケットボールのシュート
ゴールに向かってボールを蹴るとき、選手は無意識のうちに角度を計算しています。
平行に並んだラインやゴールポストの間にできる角度をうまく利用することで、最適な軌道を描けるのです。
コーチや分析スタッフが映像を解析するときにも、同位角や錯角を使って選手の動きを分析することがあります。
ビリヤードやカーリングの戦術
ビリヤードでボールを狙うとき、玉突き台の縁に平行に並ぶラインを意識しながら角度を決めます。
このとき使われるのが対頂角や錯角の考え方です。
同様に、カーリングでも氷の上に引かれた平行線を基準に、石の投げ方を戦略的に考えます。
カメラ撮影やデザイン
写真を撮るとき、建物や道のラインが傾いていると「違和感のある写真」になってしまいます。
そこでカメラマンは、平行線の性質や同位角の位置を意識してアングルを決めます。
デザインやアートの世界でも、幾何学的な美しさを表現するために角の性質が意識的に使われています。
将来の職業と平行線・角の性質

角の性質は、将来の仕事にも直結しています。
建築や土木工学
ここまでの説明の中でもたびたび出てきていますが、建築士や土木技師は、建物や橋を設計するときに角度の性質を活用します。
例えば、橋脚を地面に垂直に立てるとき、対頂角や同位角の等しさを利用して正確に測定します。
もし角度がずれていれば、大きな構造物が倒壊する危険性があります。
測量や地図作成
測量士は、土地の境界を測るときに平行線と角の性質を利用します。
遠くにある山や建物の位置を測定する際も、錯角の性質を用いて角度を計算し、正確な位置を割り出します。
これは古代から使われてきた技術であり、現代のGPS技術の基盤にもつながっています。
科学技術と工学分野
機械設計やロボット工学の分野では、部品同士の配置を正確に保つために平行線や角の性質が欠かせません。
例えば、自動車の車輪が正しく取り付けられているかを確認するには、平行性と角度の一致が重要です。
角度がわずかにずれるだけで走行性能に大きな影響が出るため、錯角や同位角の性質を応用した測定が必要になります。
数学的思考力を育てる角の性質

同位角・錯角・対頂角の学習を通して得られるのは、単なる知識ではありません。
それ以上に大切なのは、論理的に考える力です。
論理的に説明する力
証明問題を通して「なぜその角が等しいのか」を説明できるようになると、筋道を立てて考える力が養われます。
これは将来、数学以外の分野でも役立ちます。
例えば、プログラミングや法律、経済などの分野では「根拠を示して結論を導く」力が求められます。
角の性質を学ぶことは、そのトレーニングの第一歩なのです。
図形認識力の向上
また、図形を見て「どの角が同位角なのか」「錯角はどこにあるのか」を見抜く力は、空間認識力を高めます。
これは建築やデザインだけでなく、日常の生活で物事を整理したり計画したりする力にもつながります。
まとめ
このページでは平行線と角の完成性について、特に「同位角」「錯角」「対頂角」に焦点を当てて解説をしてきました。
図形の問題は方程式などの問題よりも直感的に分かりやすく、暗記に頼ってしまうこともあるかもしれません。
ですが、このページ内でも説明した通り、数学的に等しいことなどを説明するには「論理的な思考や説明」が必要になります。
そのため、まずは知識を覚えるということから始めてもらっても問題ありませんが、しっかりと「なぜこの角とあの角は等しいのか?」と自分の言葉で論理的に説明できるように、深いレベルでの学習をしていくように心がけましょう。











コメント